Answer:
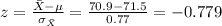
From this result we can conclude that the value of 70.9 is 0.78 deviation below the true mean of 71.5 and that can be considered as unusual. If we conduct a hypothesis test or a confidence interval we will see that we have enough evidence to conclude that the true mean is not significantly different from 71.5.
Explanation:
For this case from all the population we know that the population mean and deviation are:
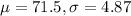
And we take a random sample of size n =40 and we got a sample mean calculated with the following formula:
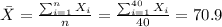
And we want to test if this value is unusually low.
Since the sample size is large n>30 we can use the central limit theorem who says that the distribution for the sample mean is given by:
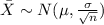
And on this case if we replace the values that we have we got:
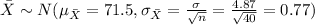
For this case we can calculate how many deviations above or below is our calculated value from the sample of size 40, using the z score given by:
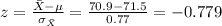
From this result we can conclude that the value of 70.9 is 0.78 deviation below the true mean of 71.5 and that can be considered as unusual. If we conduct a hypothesis test or a confidence interval we will see that we have enough evidence to conclude that the true mean is not significantly different from 71.5.