Answer:
Option (D) 49
Step-by-step explanation:
Data provided in the question:
Average underage cost,
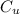 = $3.00 per sandwich
= $3.00 per sandwich
Average overage cost
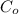 = $5.60 per sandwich
= $5.60 per sandwich
Mean = 52.1 sandwich
Standard deviation = 7.8
Now,
Critical ratio,
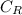 =
=
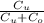
= 3 ÷ [ 3 + 5.6 ]
= 0.3488
Z value for Critical ratio = -0.389 [ From standard z value table ]
Therefore,
Order quantity to maximize profit
= Mean + Z × Standard deviation
= 52.1 + [ -0.389 × 7.8 ]
= 49
Hence,
Option (D) 49