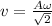Answer:
Step-by-step explanation:
General Equation of SHM is given by
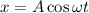
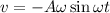
where x=position of particle
A=maximum Amplitude
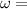 angular frequency
angular frequency
t=time
At any time Total Energy is the sum of kinetic Energy and Elastic potential Energy i.e.
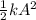
where k=spring constant
Potential Energy is given by
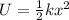
also it is given that Potential Energy(U) is equal to Kinetic Energy(K)
Total Energy
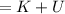
Total
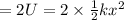
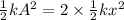
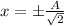
at
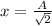
velocity is