Answer:
No. See the explanation below.
Explanation:
No. When we have the lineal model given by:
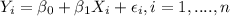
For n observations, where y represent the dependent variable, X represent the independent variable and
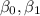 are the parameters of the model, we are assuming that
are the parameters of the model, we are assuming that
 is and independent and identically distrubuted variable that follows a normal distribution with the following parameters
is and independent and identically distrubuted variable that follows a normal distribution with the following parameters
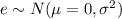 .
.
So then the expected value for any error term is
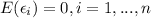
So then if we find the expected value for any observation we have this:
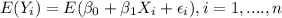
Now we can distribute the expected value on the right by properties of the expected value like this:
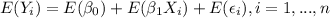
By properties of the expected value
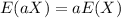 if a is a constant and X a random variable, so then if we apply this property we got:
if a is a constant and X a random variable, so then if we apply this property we got:
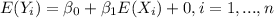
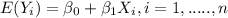
And if we see that'ts not the result supported by the claim for this reason is FALSE the statement.