Question

When asked to state the simple linear regression model, a student wrote it as follows: E(Yi) = βo + β1Xi + ei . Do you agree? Explain.

Answer 1

No. See the explanation below.

Explanation:

No. When we have the lineal model given by:

`Y_i = \beta_0 +\beta_1 X_i +\epsilon_i , i = 1,....,n`

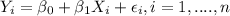
For n observations, where y represent the dependent variable, X represent the independent variable and
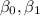`\beta_0, \beta_1` are the parameters of the model, we are assuming that
`\epsilon` is and independent and identically distrubuted variable that follows a normal distribution with the following parameters
`e\sim N(\mu=0,\sigma^2)`.

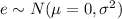So then the expected value for any error term is
`E(\epsilon_i) =0, i =1,...,n`

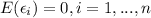
So then if we find the expected value for any observation we have this:

`E(Y_i) = E(\beta_0 +\beta_1 X_i +\epsilon_i) , i = 1,....,n`

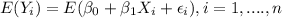
Now we can distribute the expected value on the right by properties of the expected value like this:

`E(Y_i) = E(\beta_0) +E(\beta_1 X_i) +E(\epsilon_i), i =1,...,n`

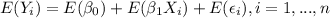
By properties of the expected value
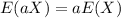`E(aX) =aE(X)` if a is a constant and X a random variable, so then if we apply this property we got:

`E(Y_i) = \beta_0 +\beta_1 E(X_i) +0 ,i=1,...,n`

`E(Y_i) =\beta_0 +\beta_1 X_i, i=1,.....,n`

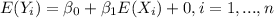
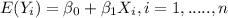
And if we see that'ts not the result supported by the claim for this reason is FALSE the statement.