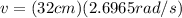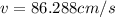Question

An air-track glider attached to a spring oscillates between the 13.0 cmcm mark and the 64.0 cmcm mark on the track. The glider completes 15.0 oscillations in 35.0 ss . What are the (a) period, (b) frequency, (c) amplitude, and (d) maximum speed of the glider

Answer 1

To solve this problem we will apply the concepts related to the Period such as the relationship between the time taken to make the oscillations, the frequency as the inverse of the period, the amplitude as the midpoint of the distance traveled and the linear velocity as the product between the velocity angular and amplitude, this is

PART A) The period would be defined by the time it takes to perform the 15 oscillations so the unit value would be

`T = (35s)/(15)`

`T = 2.33s`

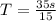
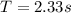
PART B) The frequency as the inverse of the period

`f = (1)/(T)`

`f = (1)/(2.33)`

`f = 0.4291Hz`

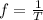
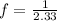
PART C) The amplitude as the midpoint of the distance traveled

`A = (d)/(2)`

`A = (64cm-13cm)/(2)`

`A = 25.5cm`

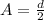
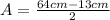
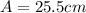
PART D) The linear velocity is the product between the amplitude and the angular frequency, then

`v= A\omega`

Where

`\omega = (2\pi)/(T)`

`\omega = (2\pi)/(2.33)`

`\omega = 2.6965rad/s`

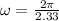
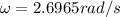
Therefore the linear velocity is

`v = (32cm)( 2.6965rad/s)`

`v = 86.288cm/s`