Answer:
Option in D is not an inverse function.
Explanation:
A. Say,
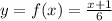
⇒ 6y = x + 1
⇒ x = 6y - 1
Here, g(x) = 6x - 1, if g(x) is the inverse function of f(x).
B. Let us assume,
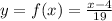
⇒ 19y = x - 4
⇒ x = 19x + 4
If g(x) is the inverse function of f(x), then, g(x) = 19x + 4
C. Let
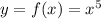
⇒
![x = \sqrt[5]{y}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ywnazxk83jeovaryrm4nli4urbwf68w2a5.png)
Here,
![g(x) = \sqrt[5]{x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/lwb73oxdiovjpfhzhidd6mczdovzgszeug.png) , if g(x) is the inverse function of f(x).
, if g(x) is the inverse function of f(x).
D. Let
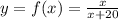
⇒ yx + 20y = x
⇒ x(y - 1) = - 20y
⇒
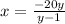
Now, if g(x) is the inverse function of f(x), then,
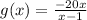
Therefore, option in D is not an inverse function. (Answer)