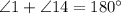Answer:
See explanation
Explanation:
1. Parallel lines t and g are cut by transversal c. Angles 1 and 9 are corresponding angles when two parallel lines t and g are cut by transversal c. By corresponding angles theorem, corresponding angles are congruent, so

2. Parallel lines c and d are cut by transversal g. Angles 9 and 14 are same-side exterior angles when two parallel lines c and d are cut by transversal g. By same-side exterior angles theorem, same-side exterior angles are supplementary (add up to 180°), so
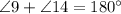
3. By substitution property,