Question

Find an equation of the circle whose diameter has endpoints (1,-4) and (-3,6).

Answer 1

`(x+1)^2+(y-1)^2=58`

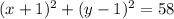
Explanation:

To find the equation of this circle, we must know the center and the radius.

We can find the radius by dividing the value of the distance formula by 2 (since
`r=(d)/(2)`):

`d=√((-3-1)^2+(6-(-4))^2)=√(116)\\r=d/2=(√(116))/(2)`

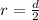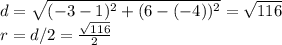
We can then find the center of the circle by averaging the coordinates:

`(1+(-3))/(2)=-1`

`(-4+6)/(2)=1`

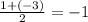
Then, we substitute these values into the equation of a circle:

`(x-(-1))^2+(y-1)^2=((√(116))/(2))^2\\(x+1)^2+(y-1)^2=58`