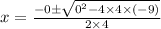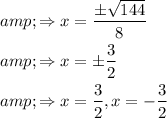Question

Solve this equation using all three methods 4x^ = 9

1.Factoring, 2. Complete the square, and 3. Using the Quadratic formula.

Answer 1

`x=-(3)/(2), x=(3)/(2)`

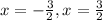
Explanation:

(1) To solve by factoring,

Given equation:
`4 x^(2)=9`

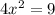
Subtract 9 from both sides of the equation.

`\begin{aligned}&4 x^(2)-9=9-9\\&4 x^(2)-9=0\\&(2 x)^(2)-3^(2)=0\\&(2 x-3)(2 x+3)=0\end{aligned}`

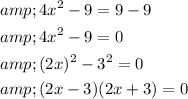
Using zero factor principle,
`2 x-3=0,2 x+3=0`

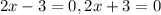
The solutions are
`x=-(3)/(2), x=(3)/(2)`.

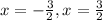(2) To solve by complete the square ,

Given
`4 x^(2)=9`

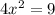
Divide both sides of the equation by 4.

`(4 x^(2))/(4)=(9)/(4)`

`\Rightarrow x^(2)=(9)/(4)`

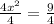
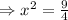
Square root on both sides.

`$\Rightarrow x=\pm (3)/(2)$`

`x=-(3)/(2), x=(3)/(2)`

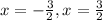
(3) To solve by quadratic formula,

`$4 x^(2)-9=0$`

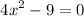
Here, a = 4, b = 0, c = –9

Quadratic formula,
`$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}$`

`x=\frac{-0 \pm \sqrt{0^(2)-4 * 4 *(-9)}}{2 * 4}`

`\begin{aligned}&\Rightarrow x=(\pm √(144))/(8)\\&\Rightarrow x=\pm (3)/(2)\\&\Rightarrow x=(3)/(2), x=-(3)/(2)\end{aligned}`