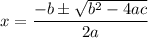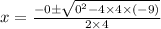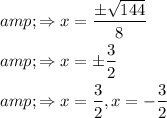Answer:
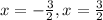
Explanation:
(1) To solve by factoring,
Given equation:
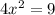
Subtract 9 from both sides of the equation.
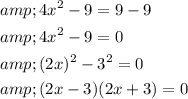
Using zero factor principle,
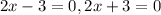
The solutions are
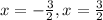 .
.
(2) To solve by complete the square ,
Given
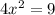
Divide both sides of the equation by 4.
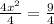
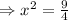
Square root on both sides.
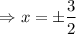
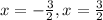
(3) To solve by quadratic formula,
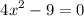
Here, a = 4, b = 0, c = –9
Quadratic formula,