Question

In the diagram

A is the point (0,-2),
B is the point (-4,2),
C is the point (0.3).
Find the equation of the line that passes through C and is parallel to AB.
I’ve had a brain blank

Answer 1

Step-by-step explanation:First find the gradient of the line:

Change in y/Change in x=y2-y1/x2-x1 y2= Second y cordinate.

=2-(-2)/(-4)-0=4/-4=-1

So the gradient is -1 :y=-x+c

'+c' is the y-intercept, which is (0,-2). So the equation of the line AB is y=-x-2.

To find the line parallel to AB that passes though C you replace the '+c' (which is -2) with the t co-ordinate of C. This gives the equation:

y=-x+3.

Answer 2

y = - x + 3

Explanation:

Parallel lines have equal slopes

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

Calculate the slope m of AB using the slope formula

m = (y₂ - y₁ ) / (x₂ - x₁ )

with (x₁, y₁ ) = A(0, - 2) and (x₂, y₂ ) = B(- 4, 2)

m=
`(2+2)/(-4-0)` =
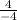`(4)/(-4)` = - 1

Thus the slope of the line going through C is m = - 1

Note C(0, 3 ) ⇒ c = 3

y = - x + 3 ← equation of line through C