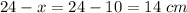Answer:
Length and width are 10 cm and 14 cm
Explanation:
If the perimeter of the square is 48 cm, then its side has length
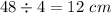
The area of the square is
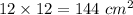
If the perimeter of the rectangle is 48 cm, then the sum of the length and the width is
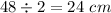
Let
Length = x cm, then
Width = 24 - x cm and the area of the rectangle is
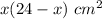
The difference of area of square and rectangle is
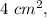 then
then
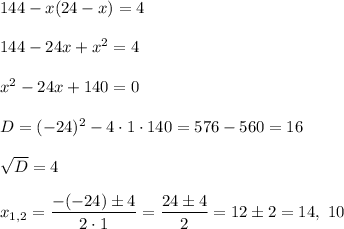
If
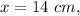 then
then
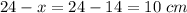 .
.
If
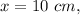 then
then