Answer:
Option 3: approximately
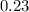 .
.
Explanation:
Let
 represent the number of circuit breakers that did not open.
represent the number of circuit breakers that did not open.
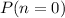 is the probability that none of the five circuit breakers did not open (i.e., all of them opened successfully.)
is the probability that none of the five circuit breakers did not open (i.e., all of them opened successfully.)
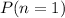 is the probability that one out of the five circuit breakers did not open.
is the probability that one out of the five circuit breakers did not open.
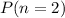 is the probability that two out of the five circuit breakers did not open.
is the probability that two out of the five circuit breakers did not open.
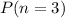 is the probability that three out of the five circuit breakers did not open.
is the probability that three out of the five circuit breakers did not open.
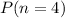 is the probability that four out of the five circuit breakers did not open.
is the probability that four out of the five circuit breakers did not open.
 is the probability that all five circuit breakers did not open.
is the probability that all five circuit breakers did not open.
There are only five circuit breakers in this circuit. As a result, these six situations represent all the possibilities that could happen to these circuit breakers. Therefore, the sum of these six possibilities should be equal to one:
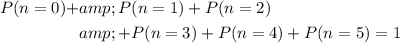 .
.
The question is asking for
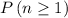 , the probability that at least one of these five circuit breakers does not open. Since
, the probability that at least one of these five circuit breakers does not open. Since
 must be an integer between
must be an integer between
 and
and
 ,
,
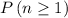 would be the same as the sum of
would be the same as the sum of
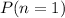 ,
,
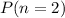 ,
,
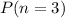 ,
,
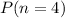 , and
, and
 . In other words,
. In other words,
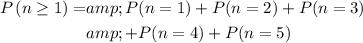 .
.
Calculating all five probabilities would likely be a very cumbersome task. That's how the following equation (which was just deduced) becomes very handy.
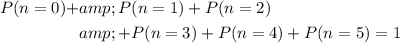 .
.
Subtract
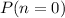 from both sides of this equality to obtain:
from both sides of this equality to obtain:
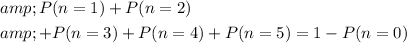 .
.
In other words, to calculate
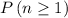 , simply finding the value of
, simply finding the value of
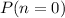 and doing a subtraction would be enough. Besides, the value of
and doing a subtraction would be enough. Besides, the value of
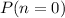 can be particularly easy to determine.
can be particularly easy to determine.
Recall that
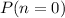 gives the probability that all five circuit breakers open successfully. The question stated that the probability for each circuit breaker to open successfully is
gives the probability that all five circuit breakers open successfully. The question stated that the probability for each circuit breaker to open successfully is
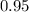 . Besides, the question assumed that the five circuit breakers work independently from each other. Hence, the probability that all five of them worked should be found with the product rule of probability:
. Besides, the question assumed that the five circuit breakers work independently from each other. Hence, the probability that all five of them worked should be found with the product rule of probability:
 .
.
Hence,
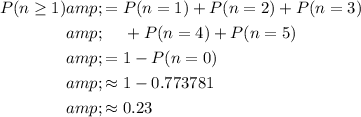 .
.