Question

Loan X has a principal of $10,000x and a yearly simple interest rate of 4%. Loan Y has a principal of $10,000y and a yearly simple interest rate of 8%. Loans X and Y will be consolidated to form Loan Z with a principal of $(10,000x 10,000y) and a yearly simple interest rate of r%, where ?

Answer 1

y=32, x=96

Explanation:

The complete question in the attached figure

we know that

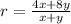`r=(4x+8y)/(x+y)` ----> given problem

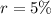`r=5\%` ----> given problem

substitute the value of r in the expression

`5=(4x+8y)/(x+y)`

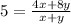
Simplify the expression

Multiply both sides by (x+y)

`5(x+y)=4x+8y\\5x+5y=4x+8y\\5x-4x=8y-5y\\x=3y`

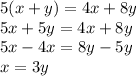
So

In the table, just look for two values, one of which is three times the other

Verify each number in the table

1) For y=21 ----> x=3(21)=63

The value of 63 is not in the table

2) For y=32 ----> x=3(32)=96

The value of 96 is in the table

3) For y=51 ----> x=3(51)=153

The value of 153 is not in the table

4) For y=64 ----> x=3(64)=192

The value of 192 is not in the table

5) For y=81 ----> x=3(81)=243

The value of 243 is not in the table

6) For y=96 ----> x=3(96)=288

The value of 288 is not in the table

therefore

y=32, x=96