Question

A revolutionary war cannon, with a mass of 2090 kg, fires a 16.7 kg ball horizontally. The cannonball has a speed of 113 m/s after it has left the barrel. The cannon carriage is on a flat platform and is free to roll horizontally. What is the speed of the cannon immedi-ately after it was fired?

Answer in units of m/s

The same explosive charge is used, so the total energy of the cannon plus cannonball system remains the same. Disregarding friction, how much faster would the ball travel if the cannon were mounted rigidly and all other parameters re-mained the same?

Answer 1

0.90291 m/s

0.45055 m/s

Step-by-step explanation:

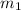`m_1` = Mass of canon = 2090 kg

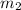`m_2` = Mass of ball = 16.7 kg

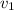`v_1` = Velocity of canon

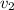`v_2` = Velocity of ball = 113 m/s

In this system the momentum is conserved

`m_1v_1=m_2v_2\\\Rightarrow v_1=(16.7* 113)/(2090)\\\Rightarrow v_1=0.90291\ m/s`

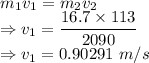
The velocity of the cannon is 0.90291 m/s

Applying energy conservation

`(1)/(2)m_1v_1^2+(1)/(2)m_2v_2^2=(1)/(2)m_2v^2\\\Rightarrow m_1v_1^2+m_2v_2^2=m_2v^2\\\Rightarrow v_2=\sqrt{(m_1v_1^2+m_2v_2^2)/(m_2)}\\\Rightarrow v_2=\sqrt{(2090* 0.90291^2+16.7* 113^2)/(16.7)}\\\Rightarrow v_2=113.45055\ m/s`

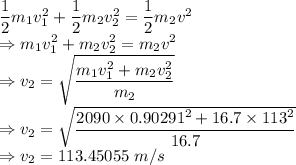
The ball would travel 113.45055-113 = 0.45055 m/s faster