Answer:
0.90291 m/s
0.45055 m/s
Step-by-step explanation:
 = Mass of canon = 2090 kg
= Mass of canon = 2090 kg
 = Mass of ball = 16.7 kg
= Mass of ball = 16.7 kg
 = Velocity of canon
= Velocity of canon
 = Velocity of ball = 113 m/s
= Velocity of ball = 113 m/s
In this system the momentum is conserved
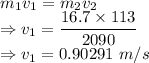
The velocity of the cannon is 0.90291 m/s
Applying energy conservation
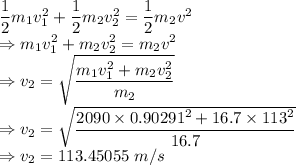
The ball would travel 113.45055-113 = 0.45055 m/s faster