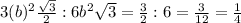Answer:
The fraction is 1/4
Explanation:
we know that
The area of an equilateral triangle, using the law of sines is equal to

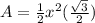
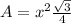
where
x is the length side of the triangle
In this problem
Let
b ----> the length side of the regular hexagon
2b ---> the length side of the equilateral triangle
step 1
Find the area of the six triangles
Multiply the area of one triangle by 6
![A=6[x^(2)(√(3))/(4)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/fp93nm75y1sweecln756cfwglimshjpsva.png)
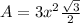
we have
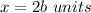
substitute
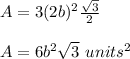
step 2
Find the area of the regular hexagon
Remember that, a regular hexagon can be divided into 6 equilateral triangles
so
The area of the regular hexagon is the same that the area of 6 equilateral triangles
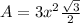
we have
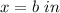
substitute

step 3
To find out what fraction of the total area of the six triangles is the area of the hexagon, divide the area of the hexagon by the total area of the six triangles