Question

16. By how much leeway (both percentage and mass) would you have in the selection of the mass of the object in the previous problem if you did not wish the new period to be greater than 2.01 s or less than 1.99 s?

Please show all of your work.

Answer 1

Here is the solution for previous question

`\\ \rm\rightarrowtail T=2\pi\sqrt{(m)/(k)}`

`\\ \rm\rightarrowtail T\propto √(m)`

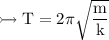
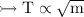
Hence

`\\ \rm\rightarrowtail (T_1)/(T_2)=\sqrt{(m1)/(m2)}`

`\\ \rm\rightarrowtail (1.5)/(2)=\sqrt{(0.5)/(m2)}`

`\\ \rm\rightarrowtail 0.75^2=(0.5)/(m2)`

`\\ \rm\rightarrowtail m_2=(0.5)/(0.75^2)`

`\\ \rm\rightarrowtail m_2=0.888888888\dots`

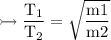
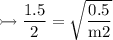
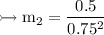
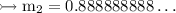
So

from this

So it's infinite in terms of 8 so must be greter than one 8

We rounded it up for 3 decimals

• 0.889kg

So

Error range=[1.99,2.01]

• ∆Error=2.01-1.99=0.02

Very mere one

Now find percentage

`\\ \rm\rightarrowtail (0.02)/(2)(100)=0.01(100)=1\%`

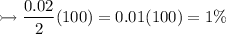
Mass should be lied in

• 0.01(0.889)=0.00889 kg

But for increase mass

it would be

• 0.00889-0.00500=0.00389kg