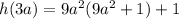Question

Evaluate the function h (x) = x^4 + x^2 + 1 at the given values of the independent variable and simplify.

a. h(3)
b. h(- 1)
c. h(-x)
d. h(3a)

Answer 1

The values are

a)
`h(3)=91`

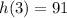
b)
`h(-1)=3`

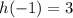
c)
`h(-x)=x^4+x^2+1=h(x)`

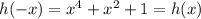
d)
`h(3a)=9a^2(9a^2+1)+1`

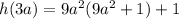
Explanation:

Given that the function h is defined by

`h(x)=x^4+x^2+1`

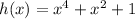
To find

a) h(3)

Put x=3 in the given function
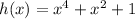`h(x)=x^4+x^2+1` we get

`h(3)=3^4+3^2+1`

`=81+9+1`

`=91`

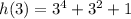
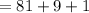
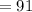
Therefore
`h(3)=91`

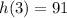
b) h(-1)

Put x=-1 in the given function
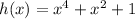`h(x)=x^4+x^2+1` we get

`h(-1)=(-1)^4+(-1)^2+1`

`=1+1+1`

`=3`

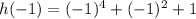
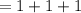
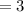
Therefore
`h(-1)=3`

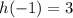
c) h(-x)

Put x=-x in the given function
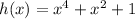`h(x)=x^4+x^2+1` we get

`h(-x)=(-x)^4+(-x)^2+1`

`=x^4+x^2+1`

`=h(x)`

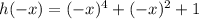
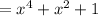
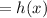
Therefore
`h(-x)=x^4+x^2+1=h(x)`

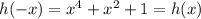
d) h(3a)

Put x=3a in the given function
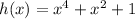`h(x)=x^4+x^2+1` we get

`h(3a)=(3a)^4+(3a)^2+1`

`=3^4.a^4+3^2.a^2+1`

`=81a^4+9a^2+1`

`=9a^2(9a^2+1)+1`

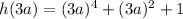
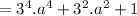
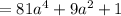
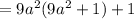
Therefore
`h(3a)=9a^2(9a^2+1)+1`