Question

A 95% confidence is given by (15,20) . The interval is based on a sample of size n=25 .

If we want to reduce the margin of error by half, we need to:

a. double the sample size.

b. quadruple the sample size.

Answer 1

b. quadruple the sample size.

Explanation:

Given that a 95% confidence is given by (15,20) .

this implies that mean = average of lower and higher bounds of confidence interval =
`(15+20)/(2) =17.5`

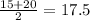
Margin of error = Upper bound - Mean =
`20-17.5 = 2.5`

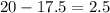
Confidence level = 95%

Critical value = 1.96

Std error =
`(2.5)/(1.96) =1.27551`

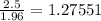
Std devition = Std error * sqrt n = 6.3775

If we want to reduce margin of error by half we must get margin of error as 1.25

For that std error for same critical value = 0.63775

Std deviation did not change

So sample size only changed which implies that sample size is 4 times the original

b. quadruple the sample size.