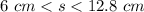Question

An acute triangle has two sides measuring 8 cm and 10cm. What is the best possible range of values for the third side, s?

Answer 1

6 < s < 12.8

Explanation:

I saw that 12.8x12.8 equals 163.84 so if the number was any higher than it would go over 164 which is the sum of the squares of 8 and 10. Since it asked for an acute triangle we must have the square of s be less than 164.

Answer 2

The range of the possible values for the third side s is the interval (6,12.8)

`6\ cm < s < 12.8\ cm`

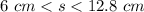
see the explanation

Explanation:

we know that

The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side

Let

s ----> the length of the third side of the triangle

Applying the Triangle Inequality Theorem

1)

`8+10 > s`

`18 > s`

`s< 18\ cm`

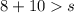
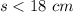
2)

`s+8>10`

`s > 10-8`

`s > 2\ cm`

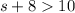
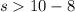
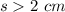
therefore

The range of the possible values for the third side s, applying the triangle inequality theorem is the interval (2,18)

`2\ cm < s < 18\ cm`

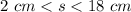
All real number greater than 2 centimeters and less than 18 centimeters

Remember that

Applying the Pythagorean theorem

In an acute triangle

`c^2 <a^2+b^2`

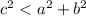
First case

c=10 cm,a=8 cm, b=s

`10^2 <8^2+s^2\\36<s^2\\s>6\ cm`

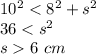
Second case

a=8 cm,b=10 cm, c=s

`s^2 <8^2+10^2\\s^2 <164\\s<12.8\ cm`

The range of the possible values for the third side s, applying the Pythagorean Theorem is the interval (6,12.8)

therefore

The range of the possible values for the third side s, is the interval (6,12.8)

`6\ cm < s < 12.8\ cm`