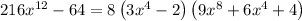Question

What is the factorization of 216x^12 -64​

Answer 1

The factorization of given expression is:

`216x^(12)-64 = 8\left(3x^4-2\right)\left(9x^8+6x^4+4\right)`

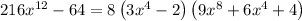
Solution:

Given that we have to factorize the given expression

Given expression is:

`216x^(12)-64`

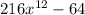
Let us factorize the expression

`\text{ Rewrite } 64 \text{ as } 8 * 8`

`\text{Rewrite } 216 \text{ as } 8 * 27`

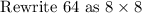
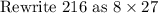
Thus the given expression becomes,

`216x^(12) - 64 = (8 * 27)(x^(12)) - (8 * 8)\\\\\text{Factor out common term 8 }`

`216x^(12) -64= 8(27x^(12)-8)`

`\mathrm{Rewrite\:}27x^(12)-8\mathrm{\:as\:}\left(3x^4\right)^3-2^3`

`8(27x^(12)-8) = 8(\left(3x^4\right)^3-2^3)`

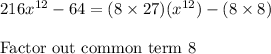
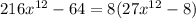
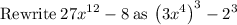
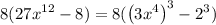
Let us apply the difference of cubes formula

`x^3-y^3=\left(x-y\right)\left(x^2+xy+y^2\right)`

`\left(3x^4\right)^3-2^3=\left(3x^4-2\right)\left(3^2x^8+2\cdot \:3x^4+2^2\right)`

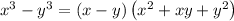
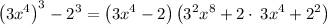
Therefore,

`8(27x^(12)-8) = 8\left(3x^4-2\right)\left(3^2x^8+2\cdot \:3x^4+2^2\right)\\\\8(27x^(12)-8) = 8\left(3x^4-2\right)\left(9x^8+6x^4+4\right)`

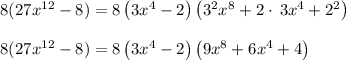
Thus factorization of given expression is:

`216x^(12)-64 = 8\left(3x^4-2\right)\left(9x^8+6x^4+4\right)`