Question

The magnitudes of the vectors are F = 84 N and P = 77 N. They act at angles theta = 47 deg and phi = 52 deg. Find the angle between the resultant of the two forces and the x-axis in deg. (Note: these values may be different from above!)

Answer 1

Step-by-step explanation:

Force, F = 84 N at 47°

Force, P = 77 N at 52°

First write the forces in vector form

`\overrightarrow{F}=84\left ( Cos47\widehat{i}+Sin47\widehat{j} \right )`

`\overrightarrow{F}=57.3\widehat{i}+61.4\widehat{j}`

`\overrightarrow{P}=77\left ( Cos52\widehat{i}+Sin52\widehat{j} \right )`

`\overrightarrow{P}=47.4\widehat{i}+60.7\widehat{j}`

Let R be the resultant of two forces.

`\overrightarrow{R} = \overrightarrow{F} + \overrightarrow{P}`

`\overrightarrow{R}=(57.3+47.4)\widehat{i}+(61.4+60.7)\widehat{j}`

`\overrightarrow{R}=104.7\widehat{i}+122.1\widehat{j}`

Let it makes an angle θ from X axis

`tan \theta =(122.1)/(104.7)`

θ = 49.4°

Answer 2

The angle between the resultant of the two forces and the x-axis is 56.93°.

Step-by-step explanation:

Given that,

Magnitude of the vector F = 84 N

Magnitude of the vector P = 77 N

Angle for F= 47°

Angle for P = 52°

We need to calculate the resultant vector

Using formula of resultant vector

`\vec{R}=\vec{F}+\vec{P}`

`\vec{R}=85(\cos47i+\sin47j)+77(\cos52i+\sin52j)`

`\vec{R}=85\cos47+77\cos52+85\sin47+77\sin52`

`\vec{R}=105.35i+122.84j`

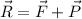
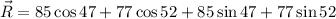
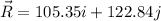
We need to calculate the magnitude

`R=√((105.35)^2+(122.84)^2)`

`R=161.82\ N`

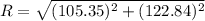
We need to calculate the angle between the resultant of the two forces and the x-axis

Using formula of angle

`\tan\theta=(R)/(105.34)`

`\theta=\tan^(-1)((R)/(105.34))`

Put the value into the formula

`\theta=\tan^(-1)((161.82)/(105.34))`

`\theta=56.93^(\circ)`

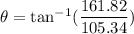
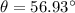
Hence, The angle between the resultant of the two forces and the x-axis is 56.93°.