Answer:
The angle between the resultant of the two forces and the x-axis is 56.93°.
Step-by-step explanation:
Given that,
Magnitude of the vector F = 84 N
Magnitude of the vector P = 77 N
Angle for F= 47°
Angle for P = 52°
We need to calculate the resultant vector
Using formula of resultant vector
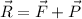
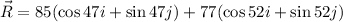
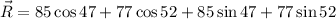
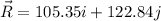
We need to calculate the magnitude
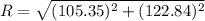
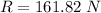
We need to calculate the angle between the resultant of the two forces and the x-axis
Using formula of angle
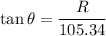
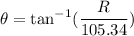
Put the value into the formula
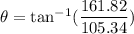
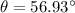
Hence, The angle between the resultant of the two forces and the x-axis is 56.93°.