Question

A large company is considering opening a franchise in St. Louis and wants to estimate the mean household income for the area using a simple random sample of households. Based on information from a pilot study, the company assumes that the standard deviation of household incomes is σ = $7,200. Of the following, which is the least number of households that should be surveyed to obtain an estimate that is within $200 of the true mean household income with 95 percent confidence?

Answer 1

the answer is actually 5,200

source: ap stats quiz and quizlet

Answer 2

4979 is the least number of households that should be surveyed to obtain an estimate that is within $200 of the true mean household income with 95 percent confidence.

Explanation:

We are given the following in the question:

Standard Deviation, σ = $7,200

Margin of error =
`\pm\$200`

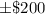
We have to find the least number of households that should be surveyed to obtain an estimate that is within $200.

Formula:

`\text{Margin of error} = \text{Test Statistic}* (\sigma)/(√(n))`

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

`1.96* (7200)/(√(n)) < 200\\\\n > (1.96* 7200)/(200) = 4978.7 \approx 4979`

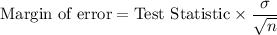
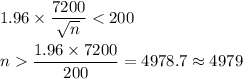
4979 is the least number of households that should be surveyed to obtain an estimate that is within $200 of the true mean household income with 95 percent confidence.