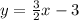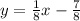Answer:
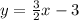
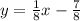
Explanation:
The given system is
3x-2y=6
0.4(20y+15)=x
The slope intercept form is y=mx+c.
For the first equation, 3x-2y=6, we add -3x to both side -2y=-3x+6
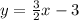
For 0.4(20y+15)=x, we expand to get:
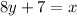
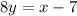
Divide through by 8
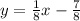
Therefore the system in slope-intercept form is: