Question

The warranty for a particular system on a new car is 2 years. During which there is no limit to the number of warranty claims per car. Historically, the average number of claims per car during the period is 0.8 claims. What type of distribution could be used to model the number of warranty claims per car?

Answer 1

Answer: by using Poisson distribution

The warranty for a particular system on a new car is 2 years

P(x=2)= 0.143

There is no limit to the number of warranty claims per car

P(X=0) = 0.449

Explanation:

step:-1

A random variable X is said to follow a Poisson distribution if it assumes only non-negative values and its probability distribution is given by

P(X=x) =
`(e^(-w)w^(x)  )/(x!)`

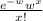
here w>0 is called the parameter of the distribution

Step 2:- Given mean value of Poisson distribution = 0.8

The warranty for a particular system a new car is 2 years

P(X=x)=P(X=2)=
`\frac{e^(-0.8){0.8^(2) }  }{2!}`

P(x=2)= 0.143

Step 3:-

Given mean value of Poisson distribution = 0.8

There is no limit to the number of warranty claims per car

P(X=x)=P(X=0)=
`\frac{e^(-0.8){0.8^(0) }  }{0!}`

P(X=0) = 0.449