The value of
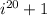 is 2
is 2
The value of
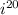 + 1 can be determined by considering the powers of the imaginary unit i
+ 1 can be determined by considering the powers of the imaginary unit i
The powers of i follow a cycle:
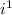 = i,
= i,
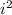 = -1,
= -1,
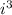 = -i, and
= -i, and
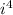 = 1. After
= 1. After
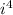 , the powers repeat.
, the powers repeat.
Since(20 is a multiple of 4, we know that
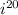 will be equivalent to
will be equivalent to
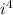 , which is 1.
, which is 1.
Therefore,
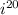 + 1 = 1 + 1 = 2
+ 1 = 1 + 1 = 2
So, the value of
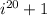 is 2
is 2