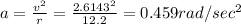Answer:
(a) 0.2165 rad/sec
(b) 2.6143 m /sec
(C)
Step-by-step explanation:
It is given that wheel rotates each revolution in 29 sec
So time period T = 29 sec
(a) Angular speed is equal; to
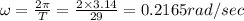
(b) Radius is given r = 12.2 m
So linear velocity
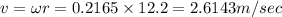
(C) Angular acceleration is given by