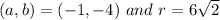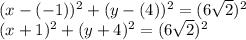Answer:
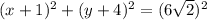
Explanation:
The length of the diameter
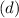 will be the distance between
will be the distance between

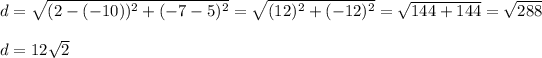
Radius:
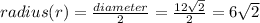
Centre:
Let
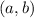 be centre of the circle.
be centre of the circle.
Centre will be the mid point of end points of diameter.
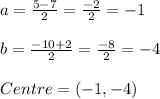
Equation of circle:
If
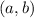 be centre and
be centre and
 be the radius.
be the radius.
Equation of circle:
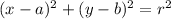
Here