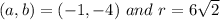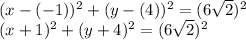Question

The endpoints of a diameter of a circle are (5,-10) and (-7,2). What is the equation of the circle in standard form?

Answer 1

`(x+1)^2+(y+4)^2=(6√(2))^2`

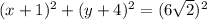
Explanation:

The length of the diameter
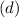`(d)` will be the distance between
`(5,-10)\ and\ (-7,2).`

`d=√((2-(-10))^2+(-7-5)^2)=√((12)^2+(-12)^2)=√(144+144)=√(288)\\\\d=12√(2)`

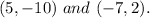
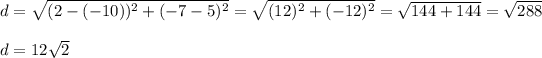
Radius:

`radius(r)=(diameter)/(2)=(12√(2))/(2)=6√(2)`

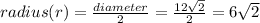
Centre:

Let
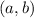`(a,b)` be centre of the circle.

Centre will be the mid point of end points of diameter.

`a=(5-7)/(2)=(-2)/(2)=-1\\\\b=(-10+2)/(2)=(-8)/(2)=-4\\\\Centre=(-1,-4)`

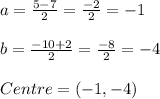
Equation of circle:

If
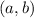`(a,b)` be centre and
`r` be the radius.

Equation of circle:
`(x-a)^2+(y-b)^2=r^2`

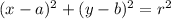
Here
`(a,b)=(-1,-4)\ and\ r=6√(2)`

`(x-(-1))^2+(y-(4))^2=(6√(2))^2\\(x+1)^2+(y+4)^2=(6√(2))^2`