Option A, B, C
(-4, -3) and (1, 6) and (2, 4) is a solution to given system of inequalities
Solution:
Given system of inequalities are:
Line 1 : 3y < 2x + 18
Line 2 : -4y < -x + 12
Let us substitute the given solution set in options and check if it satisfies both the inequalities
Option A
Substitute x = -4 and y = -3 in Line 1
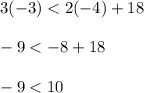
-9 less than 10 is true
Substitute x = -4 and y = -3 in Line 2
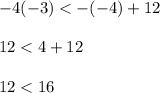
12 less than 16 is true
Thus (-4, -3) is a solution to given system of inequalities
Option B
Substitute x = 1 and y = 6 in line 1
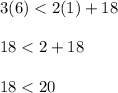
18 less than 20 is true
Substitute x = 1 and y = 6 in line 2
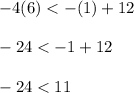
-24 is less than 11 is true
Thus (1, 6) is a solution to given system of inequalities
Option C
Substitute x = 2 and y = 4 in line 1
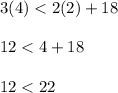
12 is less than 22 is true
Substitute x = 2 and y = 4 in line 2
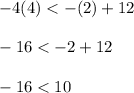
-16 less than 10 is true
So, (2, 4) is a solution to given system of inequalities
Option D
Substitute x = 5 and y = -5 in line 1
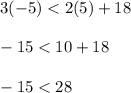
-15 is less than 28 is true
Substitute x = 5 and y = -5 in line 2
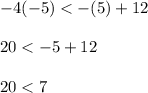
20 less than 7 is not true
Thus (5, -5) is not a solution to given system of inequalities
Option E
Substitute x = 3 and y = 2 in line 1
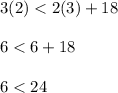
6 less than 24 is not true
Thus (3, 2) is not a solution to given system of inequalities