Question

Refer to the technology output given to the right that results from measured hemoglobin levels (g/dL) in 100 randomly selected adult females. The Tntrval confidence level of 90% was used. 13.032,13.418) x= 13.225 a. Express the confidence interval in the format that uses the "less than" symbol. Assume that the original listed data use two decimal places, andSx-1.164 round the confidence interval limits accordingly. b. Identify the best point estimate of μ and the margin of error. c. In constructing the confidence interval estimate of μ, why is it not necessary to confirm that the sample data appear to be from a population with a normal distribution?

Answer 1

Explanation:

a)

Confidence interval in less than symbol expressed as

`\bar{x} - E < \mu < \bar{x} + E`

Where
`\bar{x}` is sample mean and
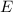`E` is margin of error.

`13.03 < \mu 13.42`

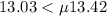
b)

The given t interval is
`(13.032 , 13.418 )`

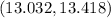
That is
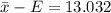`\bar{x} - E = 13.032` and
`\bar{x} + E = 13.418`

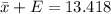
Solve these two equation by adding together.

`2 \bar{x} = 13.032 + 13.418 \\\\\bar{x} = 13.225`

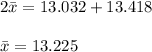
Solve this value of \bar{x} in equation
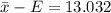`\bar{x} - E = 13.032` and solve for
`E`

`13.225 - E = 13.032 \\\\E = 0.193`

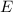
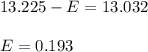
Best point estimate of
`\mu = \bar{x} = 13.225`

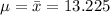
Best point estimate of margin of error = 0.193

c)

Since sample size = 100 which is sufficiently large (Greater than 30) , it is no need to confirm that

sample data appear to be form a population with normal distribution.