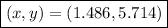Question

Recall the equation for a circle with center (h,k) and radius r. At what point in the first quadrant does the line with equation y

=2.5x+2 intersect the circle with radius 4 and center (0, 2)?

Answer 1

At point (1.486, 5.714)

Explanation:

The equation of the circle with radius 4 and center at (0, 2) is:

`x^2+(y-2)^2=16`

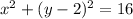
and we want to know where in the 1st quadrant does it intersect with line
`y=2.5x+2`

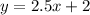
To find the point of intersection we put the value of
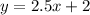`y=2.5x+2` into the equation of the circle:

`x^2+((2.5x+2)-2)^2=16`

`x^2+(2.5x)^2=16`

`7.25x^2=16`

`x=\pm 1.486`

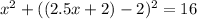
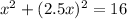
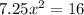
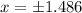
and since we only concerned with the 1st quadrant we take the positive value of
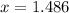`x=1.486` which is the x coordinate of intersection.

The y coordinate is found by putting this x value into either the circle equation or the line equation ; we choose the line equation
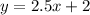`y=2.5x+2` because it is easier to work with.

`y=2.5(1.486)+2=5.714`

`\boxed{y=5.714}`

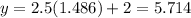
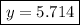
Thus we have the point of intersection

`\boxed{(x,y)=(1.486, 5.714)}`