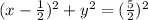Answer:
The equation for the circle is:
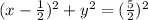
Explanation:
Here, let us assume the two end points of the diameter are:
P (3,-1) and Q (-2,-1)
Now, as we knew diameter is the chord that passer through the center of the circle.
⇒ Mid point of DIAMETER = Center coordinates of the Circle
Let us assume O(x,y) is the center of the line segment PQ.
So, by MID POINT FORMULA:
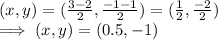
⇒ The center coordinates of the circle = O(0.5,-1) ...... (1)
Now, RADIUS = Half of DIAMETER
Using DISTANCE FORMULA:
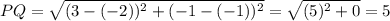
So, Radius = 5/2 = 2.5 units
Now, the equation of circle with radius r and center coordinate ( h,k) is given as:
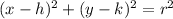
Substitute r = 2.5 and (h,k) = (0.5,0) we get:
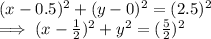
Hence the equation for the circle is: