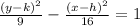Question

Write the equation of a hyperbola with foci at (3, -3) and (3, 7) and vertices at (3, -1) and (3, 5).

Answer 1

The answer to your question is

`((y - k)^(2))/(9) - ((x - h)^(2) )/(16) = 1`

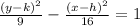
Explanation:

See the picture below

- From the picture we conclude that it is a vertical hyperbola

Center = (3, 2)

c = 5

a = 3 b² = c² - a² b² = 5² - 3² b² = 25 - 9 b² = 16

b = 4

- Equation

`((y - k)^(2))/(a^(2) ) - ((x - h)^(2) )/(b^(2)) = 1`

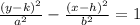
- Substitution

`((y - 2)^(2))/(3^(2) ) - ((x - 3)^(2))/(4^(2)) = 1`

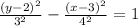
- Result

`((y - k)^(2))/(9) - ((x - h)^(2) )/(16) = 1`