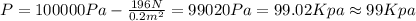Answer:
a)
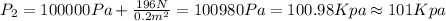
b)
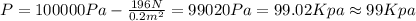
Step-by-step explanation:
Let's consider the piston on the figure attached.
We know that the atmospheric pressure on this case is
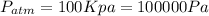
We know that the Are of the piston is
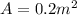 and we have also the mass
and we have also the mass
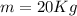
Part a
We want to find the pressure at the gas, so that means point 2, and we assume that the pressure on any point of the gas is constant and the same. So then we can find the pressure at point 2 like this:
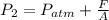
And the force on this case is the weigth
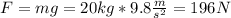
And then we have:
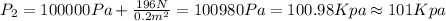
Part b
For this case we want to find the pressure if the device were changed and now would be upside down. On this case we will have lower pressure than from part a and would be given by: