Question

Número 60 de la siguiente sucesión 8, 5, 2, -1, -4

Answer 1

`\huge\boxed{\bf\:a_(n) = 185}`

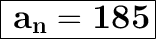
Explanation:

Consider the following sequence as an arithemetic progression (AP). Here, we need to find the 60th term of the given AP.

According to the AP,

• First term (a) = 8
• Common difference (d) =
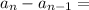  `a_(n) - a_(n - 1) =` 8 - 5 = 3
• Number of terms (n) = 60
• Last term
  `(a_(n)) = \: ?`

Now, use the formula →
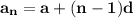`\bf\: a_(n) = a + (n - 1) d` & substitute the values in it to find the value of '
`a_(n)`'.

`a_(n) = a + (n - 1) d\\a_(n) = 8 + (60 - 1)3\\a_(n) = 8 + (59*3)\\a_(n) = 8 + 177\\\boxed{\bf\:a_(n) = 185}`

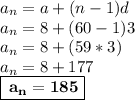
The value of '
`a_(n)`' in the given AP is 185.

`\rule{150pt}{2pt}`