Question

If f(x) and its inverse function, f Superscript negative 1 Baseline (x), are both plotted on the same coordinate plane, where is their point of intersection?

Answer 1

C

Explanation:

2, 2

Answer 2

(2,2)

Explanation:

step 1

Find the equation of f(x)

is a line that passes through the points (0,6) and (3,0)

Find the slope

`m=(0-6)/(3-0)=-2`

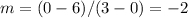
The function f(x) in slope intercept form is equal to

`f(x)=-2x+6`

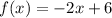
step 2

Find the inverse

Let y=f(x)

`y=-2x+6`

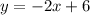
Exchange the variables x for y and y for x

`x=-2y+6`

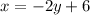
Isolate the variable y

`2y=-x+6`

`y=-0.5x+3`

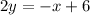
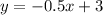
Let

`f^(-1)(x)=y`

`f^(-1)(x)=-0.5x+3`

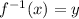
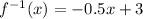
step 3

Solve the system of equations

`f(x)=-2x+6`

`f^(-1)(x)=-0.5x+3`

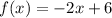
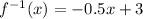
equate both functions

`-0.5x+3=-2x+6`

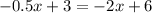
solve for x

`2x-0.5x=6-3`

`1.5x=3`

`x=2`

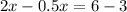
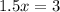
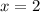
substitute the value of x in any of the functions

`f(x)=-2(2)+6=2`

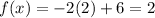
The solution is the point (2,2)

therefore

Their point of intersection is (2,2)