Answer:
(2,2)
Explanation:
step 1
Find the equation of f(x)
is a line that passes through the points (0,6) and (3,0)
Find the slope
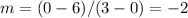
The function f(x) in slope intercept form is equal to
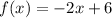
step 2
Find the inverse
Let y=f(x)
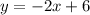
Exchange the variables x for y and y for x
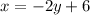
Isolate the variable y
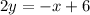
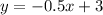
Let
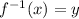
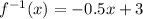
step 3
Solve the system of equations
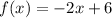
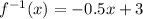
equate both functions
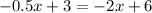
solve for x
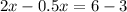


substitute the value of x in any of the functions
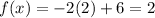
The solution is the point (2,2)
therefore
Their point of intersection is (2,2)