Answer:
51.96 feet is the value with which the seat on the rim is rising in the vertical direction
Explanation:
Angular velocity = ω= 2 rad/s
radius of ferris wheel = r = 30 feet
We need to find that , how fast is a seat on rim rising (in vertical direction) when it is 15 feet above horizontal line through center of wheel, meaning how quickly a point on rim of wheel is rising vertically at point where this point is 15 ft above horizontal line through center of wheel.
To write the expression :
y = r sin (ω t)
y= 30 sin (2t)
y = 60 sin(t) cos(t)
y= 60

y = 60 cos(2t) _____________________(Equation 1)
The position of 15 feet up is given by angle of 2t
Sin (2t) =
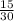 =
=

Then,
2t = 30 degrees
cos (2t) = cos (30) =
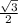
put in equation 1 , we get:
y = 60cos(30)
y = 60 (0.866)
y= 51.96 feet
which is the value with which the seat on the rim is rising in the vertical direction when it is 15 feet above horizontal line through center of wheel.