Question

Determine the values of k such that the system of linear equations does not have a unique solution. (Enter your answers as a comma-separated list.) x + y + kz = 6 x + ky + z = 3 kx + y + z = 9.

Answer 1

k = 1 ,k = - 2

Step-by-step explanation:

Given that

x + y + k z = 6

x + k y + z = 3

k x + y + z = 9

If the determinate of given equation is zero then the above linear equation do not have a unique solution.

`\begin{bmatrix}1 & 1 & k\\ 1 & k & 1\\ k & 1 & 1\end{bmatrix}=0`

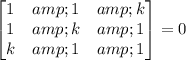
Lest solve the above determinate

(k - 1 ) - (1 - k) + k( 1 - k²) = 0

K - 1 - 1 + k+ k - k³ = 0

3 k - 2 - k³ = 0

k³ - 3 k + 2 = 0

(k - 1 ) ( k² + k - 2 ) = 0

( k - 1 )(k -1 )(k+2) = 0

k = 1 ,k = - 2

That is why the value of k will be 1 and - 2 .