Question

For a normal distribution, find the percentage of data that area) within 1 standard deviation of the meanb) to the right of 1.5 standard deviations below the meanc) more than 0.5 standard deviations away from the mean

Answer 1

a) 68%.

b) 93.3%

c) 61.7%

Explanation:

#platolivesmatter

Hope this helped :)

Answer 2

a) 68%.

b) 93.3%

c) 61.7%

Explanation:

We are asked to find the percentage of data under normal distribution for given boundaries.

a) The percentage of data that are within 1 standard deviation of the mean.

We will use empirical rule to solve our given problem.

Empirical rule states that approximately 68% of the data lies within one standard deviation of the mean, therefore, answer for part (a) would be 68%.

b) Since z-score represents that a data point is how many standard deviation above or below mean.

We need to find
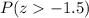`P(z>-1.5)`. We will use formula
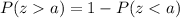`P(z>a)=1-P(z<a)` to solve our given problem.

`P(z>-1.5)=1-P(z<-1.5)`

Using normal distribution table, we will get:

`P(z>-1.5)=1-0.06681`

`P(z>-1.5)=0.93319`

`0.93319* 100\%=93.319\%\approx 93.3\%`

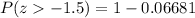
Therefore, approximately 93.3% of the data is to the right of 1.5 standard deviations below the mean.

c) We need to find
`P(z<-0.5)+P(z>0.5)`.

`P(z<-0.5)+P(z>0.5)`

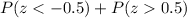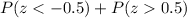
Since normal distribution is symmetric so both these values will be equal.

`0.30854+0.30854=0.61708`

`0.61708* 100\%=61.708\%\approx 61.7\%`

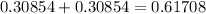
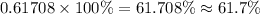
Therefore, approximately 61.7% of the data set is more than 0.5 standard deviations away from the mean.