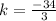Answer:
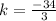
Explanation:
Step 1 :-
Perpendicular condition :-
Step 1:-
Two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.

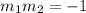
Step 2:-
The given points are (-8,k) and (-4,-8)

finding slope of the first line is
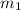
using formula
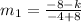
=
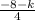
finding slope of the second line is

using formula

=
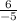
Step 3:-
using perpendicular condition
The two lines are perpendicular and their slopes are
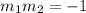

simplification,we get solution is


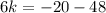
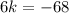
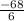
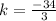
Final answer is