Question

The center of the circle shown below is at (5,4). A point on the circle is at (12,15). What is the radius of this circle? Round the answer to the nearest tenth of a unit. A. 10.0 units B. 11.0 units C. 12.0 units D.. 13.0 units

Answer 1

The correct option is D. 13.0 unit

Therefore the Radius of a Circle is 13.0 unit (nearest tenth of a unit)

Explanation:

Given:

Let C be the center of a Circle

C = (x₁ , y₁) = ( 5 , 4)

Let A be the point on a Circle

A = (x₂ , y₂) = ( 12 , 15)

To Find:

Radius, CA = ?

Solution:

Radius :

The radius of a circle is the distance from the center of the circle to any point on its Circle.

So By Distance Formula Between Two point is given as

`l(CA) = \sqrt{((x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) )}`

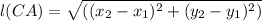
Substituting the values we get

`l(CA) = \sqrt{((12-5)^(2)+(15-4)^(2) )}`

`l(CA) = \sqrt{((7)^(2)+(11)^(2) )}`

`l(CA) = √((49+121))=√(170)=13.03\ unit`

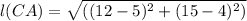
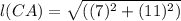
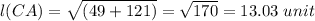
Therefore the Radius of a Circle is 13.0 unit