Question

The binomial (a+5) is a factor of a2+7a+10. What is the other factor?

(a+2)
(a+5)
(a−2)
(a−5)

Answer 1

The other factor is (a + 2)

Solution:

Given that (a + 5) is a factor of
`a^2+7a+10`

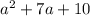
To find: the other factor

Let "x" be the other factor

So both the factors "x" and (a + 5) when multiplied must give
`a^2+7a+10`

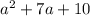
Therefore, we can say,

`x * (a+5) = a^2+7a+10\\\\x = (a^2+7a+10)/(a+5)`

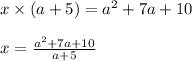
Let us factor the numerator

7a in numerator can be written as 2a + 5a

`x = (a^2+2a + 5a+10)/(a+5)`

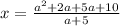
Take "a" as common from first two terms in numerator and "5" as common from last two terms in denominator

`x = (a(a+2) + 5(a+2))/(a + 5)`

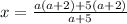
Take (a + 2) as common from numerator

`x = ((a+2)(a+5))/((a + 5))`

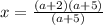
Cancel the common factors in numerator and denominator

`x = a + 2`

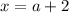
Thus the other factor is (a + 2)