Question

Two planes are circling an airport awaiting their landing clearance. If the following measures in the diagram below are correct, how far are the two planes away from each other? Find the distance from Point D to Point C. (Hint: Start by finding length AC).

A. 2800 feet


B. 4557 feet


C. 5796 feet


D. 6132 feet

Answer 1

i’m pretty sure the answer is 4557 feet :)

Answer 2

B. 4557 ft

Explanation:

In this problem we have to types of triangles. We have a right triangle and a not right triangle.

The side we have to find is part of the not right triangle, so there we would have to use the law of cosines. However, that triangle isn't complete. So, we first have to find the hypothenuse of the right triangle AC, and then apply the law of cosines for the upper triangle.

We have to apply trigonometric reasons to find the hypothenuse, because we know only one side and one angle of the right triangle. So,

`sin28\°=(1800)/(AC)\\\\ AC=(1800)/(sin28\°)=3834ft`

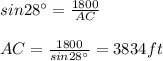
Now we have AC, we apply the law of cosines to the upper triangle ACD

`CD^(2)=AC^(2)+AD^(2)-2AC.AD.cos34\°\\ CD=\sqrt{(3834)^(2)+(7200)^(2)-2(3834)(7200)(cos34\°)}\\CD=4557ft`

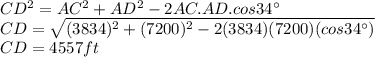
Therefore, the right answer is B. 4557 ft.