Question

At an airport radar tower, the air traffic controller was able to determine how far two planes were away from the airport and the included angle. How far were the two planes away from each other?

A. 2800 feet

B. 4000 feet

C. 5126 feet

D. 6132 feet

Answer 1

Answer: C. 5126 feet

Explanation:

Answer 2

C. 5126 feet.

Explanation:

To solve this problem, we have to apply the law of cosines.

According to the problem, the distance of the first plane to the radar tower is
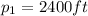`p_(1)= 2400ft` and the distance of the second plane to the radar tower is
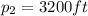`p_(2)=3200ft`. Additionally, the angle between these two distances is
`\theta = 132\°`.

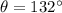So, if we apply the law of cosine, we have

`x^(2)=p_(1)^(2)+ p_(2)^(2)-2p_(1)p_(2)cos\theta`

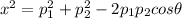
Replacing all given values, we have

`x^(2)=(2400)^(2)+ (3200)^(2)-2(2400)(3200)cos132\°\\x=√(16000000-15360000(-0.67))\approx 5127.5ft`

Therefore, the right answer is C. 5126 feet.

(The difference between digits is due to the number of decimals we used in the operations)