Question

The length of human pregnancy is known to have mean length of 268 days. A random sample of 64 pregnant women was selected and it was found that the average pregnancy length in that sample was 266 days.Which of the following is a true statement about this scenario?If a different random sample of 64 pregnant women were selected, the average pregnancy length in that sample would have to be also 266 days.(a) Both 268 and 266 are parameters(b) Both 268 and 266 are statistics(c) 268 is a parameter and 266 is a statistic(d) The recorded sample average of 266 days is clearly a mistake. It must be 268 days just like the population mean.

Answer 1

For this case we know that : The length of human pregnancy is known to have mean length of 268 days. So then this value need to represent a paramter since is related to all the population and in known
`\mu=168`

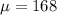
And for this case the value obtained from the sample calculated as:

`\bar x= (\sum_(i=1)^n X_i )/(n)= 266`

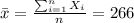
represent a statisitc (called the sample mean) in order to estimate the population mean.

So then the best option for this case is:

(c) 268 is a parameter and 266 is a statistic

Explanation:

By definition a parameter is "any numerical quantity that characterizes a given population or some aspect of it"

By definition a statistic or sample statistic is "any quantity computed from values in a sample" in order to estimate the parameter of interest.

For this case we know that : The length of human pregnancy is known to have mean length of 268 days. So then this value need to represent a paramter since is related to all the population and in known
`\mu=168`

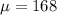
And for this case the value obtained from the sample calculated as:

`\bar x= (\sum_(i=1)^n X_i )/(n)= 266`

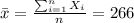
represent a statisitc (called the sample mean) in order to estimate the population mean.

So then the best option for this case is:

(c) 268 is a parameter and 266 is a statistic